NOAA Microwave Sounding Temperature Assessment System
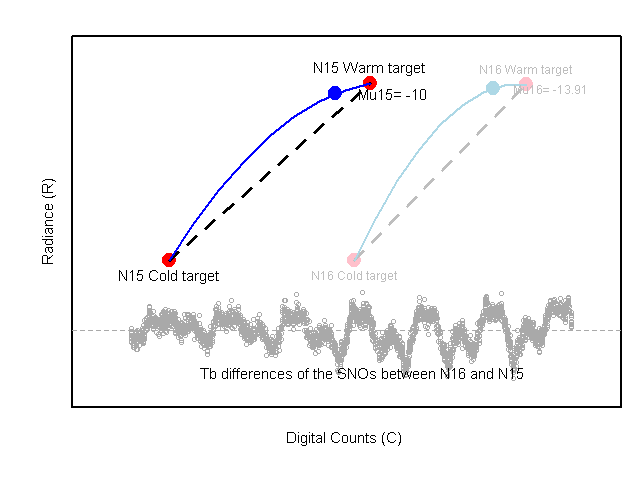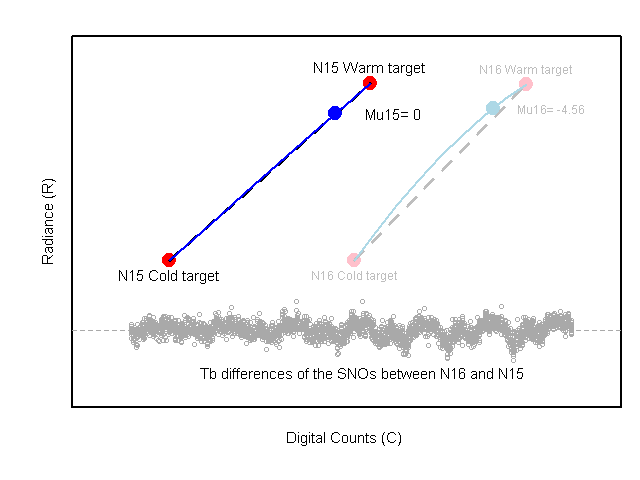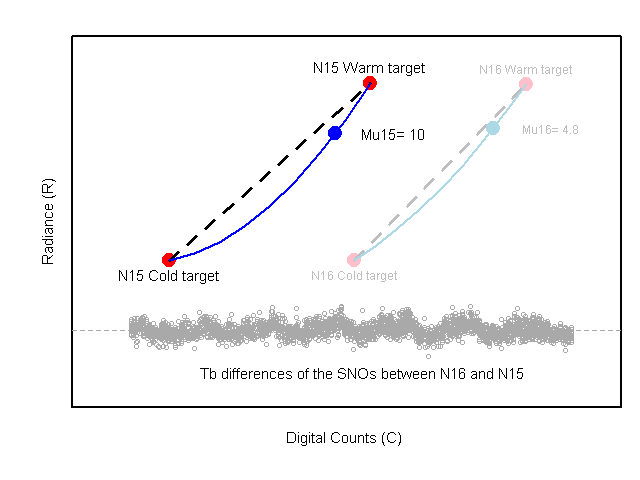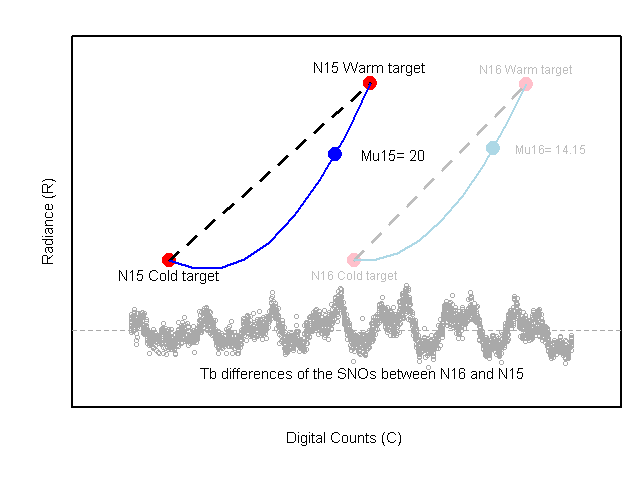
Figure 1. Animation of SNO calibration sequential procedure
Methodology
MSU uses an in-orbit calibration method that includes two calibration targets: the cosmic cold space and an onboard blackbody warm target. The cold space has a temperature of 2.73 K, and the warm target temperature is measured by the platinum resistance thermometers embedded in the blackbody target. In each scan cycle, the MSU looks at these targets as well as the earth, and the signals from these 'looks' are processed by the instrument and recorded as electric voltage in the format of digital counts. The root-level (level 1c) calibration converts the digital count of the earth scene look to the earth scene radiance using the two calibration targets as the end-point references. The calibration algorithm we use is written as:
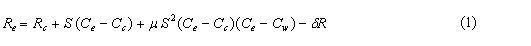
where R is the earth radiance,
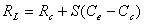 , representing
the dominant linear response, and
, representing
the dominant linear response, and
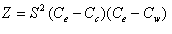 is a nonlinear response.
C represents the raw counts (electric voltage output) and
is a nonlinear response.
C represents the raw counts (electric voltage output) and
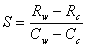 is the slope determined by the two calibration points.
The subscripts e, w and c refer to the earth-
view scene, onboard warm blackbody target, and cold space, respectively;
is the slope determined by the two calibration points.
The subscripts e, w and c refer to the earth-
view scene, onboard warm blackbody target, and cold space, respectively;
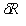 represents a radiance offset; and µ is a nonlinear coefficient. The cold
space radiance Rc is specified to be 9.6 x 10-5 mW
(sr m2 cm-1)-1 for all
scan lines. This corresponds to a brightness temperature of 4.78 K that
includes the cold-space temperature of 2.73 K plus an increase of about 2
K due to the antenna side-lobe radiation. The nonlinear coefficient is a
function of the MSU instrument body temperature but is assumed to be a
constant here since its variation range is small (Zou et al., 2006). The
algorithm to compute Rw can be found in the NOAA Polar Orbiter Data User's
Guide. Once the radiance is known, the brightness temperature, Tb, is
computed using the Planck function.
represents a radiance offset; and µ is a nonlinear coefficient. The cold
space radiance Rc is specified to be 9.6 x 10-5 mW
(sr m2 cm-1)-1 for all
scan lines. This corresponds to a brightness temperature of 4.78 K that
includes the cold-space temperature of 2.73 K plus an increase of about 2
K due to the antenna side-lobe radiation. The nonlinear coefficient is a
function of the MSU instrument body temperature but is assumed to be a
constant here since its variation range is small (Zou et al., 2006). The
algorithm to compute Rw can be found in the NOAA Polar Orbiter Data User's
Guide. Once the radiance is known, the brightness temperature, Tb, is
computed using the Planck function.
| Satellite | Channel2 | Channel3 | Channel4 | |||
|---|---|---|---|---|---|---|
| δR | µ | δR | µ | δR | µ | |
| NOAA TIROS-N | 1.3963 | 5.4062 | 5.7535 | 1.2941 | 1.6808 | 4.8256 |
| NOAA 6 | 0 | 7.3750 | 0.1162 | 6.1974 | -1.5438 | 6.5032 |
| NOAA 7 | 0.5446 | 6.6502 | -2.8131 | 10.4644 | -1.9660 | 6.5637 |
| NOAA 8 | -0.8244 | 7.5141 | 1.4737 | 4.4531 | -0.5083 | 5.5242 |
| NOAA 9 | -0.0771 | 5.9714 | 0.1026 | 9.0332 | 0.7721 | 6.1028 |
| NOAA 10 | 0 | 6.25 | 0 | 5.63 | 0 | 4.95 |
| NOAA 11 | -2.4641 | 9.5909 | -1.9983 | 7.1892 | -0.7271 | 5.4574 |
| NOAA 12 | -0.0996 | 6.7706 | -2.3979 | 8.3282 | -4.6074 | 7.1040 |
| NOAA 14 | -0.6363 | 7.4695 | -3.0810 | 8.7524 | -0.7753 | 5.4175 |
Equation (1) is a modified version of the calibration algorithm currently
running for generating NOAA MSU/AMSU operational calibrated root-level
(level-1c) radiances, where was assumed to be zero and the nonlinear
coefficient was obtained from pre-launch chamber test datasets. This pre-
launch operational calibration was conducted for each MSU/AMSU
independently. Because of the independency and orbital changes after
launch, the pre-launch calibration left residual time-changing biases on
the order of 0.5 K between satellites. To remove intersatellite biases,
the offset 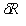 is included in equation (1) so the algorithm is allowed for
intercalibration using the SNO matchups (Zou et al., 2006). The SNO
matchups contain simultaneous observations that are less than 2 minutes
apart and within 111 km ground distance apart for the nadir pixels from
any NOAA satellite pairs. Using the SNO matchups, a sequential procedure
to obtain the calibration coefficients
is included in equation (1) so the algorithm is allowed for
intercalibration using the SNO matchups (Zou et al., 2006). The SNO
matchups contain simultaneous observations that are less than 2 minutes
apart and within 111 km ground distance apart for the nadir pixels from
any NOAA satellite pairs. Using the SNO matchups, a sequential procedure
to obtain the calibration coefficients 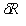 and µ was developed. This
sequential procedure is described in details in Zou et al. (2006, 2009)
and demonstrated by following animation. The obtained values for
and µ was developed. This
sequential procedure is described in details in Zou et al. (2006, 2009)
and demonstrated by following animation. The obtained values for 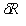 and µ for
all nine MSU instruments are listed in Table 1. By design of the
calibration procedure, these coefficients have reduced the intersatellite
biases and warm target contamination to a minimum (Zou et al. 2006, 2009).
and µ for
all nine MSU instruments are listed in Table 1. By design of the
calibration procedure, these coefficients have reduced the intersatellite
biases and warm target contamination to a minimum (Zou et al. 2006, 2009).
For the AMSU-A observations, time dependent offsets and nonlinear coefficients are introduced for certain channels to account for their bias. In specific,

is assumed for NOAA-15 channel 6, MetOp-A channel 7, and most NOAA-16 channels, where δR0 is a constant offset, κ is a constant rate of changes in the offset, t is time, and t0 is a reference time. As shown later on, this offset expression is sufficient to remove the bias drift in NOAA-16 and MetOp-A channel 7. However, it is insufficient to remove the bias drift in NOAA-15 channel 6. For this channel, the nonlinear coefficient is also assumed to be time-dependent,

where µ0 is a constant nonlinear coefficient, and λ is the rate of changes of the nonlinear coefficient, and t1 is another reference time. Table 2 shows calibration coefficients for AMSU-A channels 4-14. Aqua AMSU-A is not recalibrated using the SNO method due to the lack of level 1A products (currently only a constant offset is adjusted to its channel 6).
| δR0 | κ | µ0 | λ | ||
|---|---|---|---|---|---|
| Channel 4 | NOAA-15 | 0 | 0 | -0.269 | 0 |
| NOAA-16 | 0 | 0 | -0.718 | 0 | |
| NOAA-17 | 0.220 | 0 | -0.886 | 0 | |
| NOAA-18 | 0.276 | 0 | 0.929 | 0 | |
| MetOp-A | 0.324 | 0 | 0.442 | 0 | |
| Aqua | -0.034 | 0 | 0 | 0 | |
| Channel 5 | NOAA-15 | 0 | 0 | 0.3 | 0 |
| NOAA-16 | -1.846 | -7.248e-07 | 2.4 | 0 | |
| NOAA-17 | 0.877 | 0 | -1.007 | 0 | |
| NOAA-18 | 0 | 0 | 1.468 | 0 | |
| MetOp-A | 0.467 | 0 | 0.262 | 0 | |
| Aqua | 0.023 | 0 | 0 | 0 | |
| Channel 6 | NOAA-15 | 1.406 | -0.614e-05 | 0 | 0.442 |
| NOAA-16 | -2.903 | -1.177e-6 | 4.3 | 0 | |
| NOAA-17 | 5.056 | 0 | -3.722 | 0 | |
| NOAA-18 | 0 | 0 | 3 | 0 | |
| MetOp-A | 1.131 | 0 | 2.389 | 0 | |
| Aqua | 1.667 | 0 | 0 | 0 | |
| Channel 7 | NOAA-15 | 0 | 0 | 0.3 | 0 |
| NOAA-16 | -4.475 | -1.570e-06 | 3.6 | 0 | |
| NOAA-17 | 3.043 | 0 | -2.347 | 0 | |
| NOAA-18 | 1.319 | 0 | 0.479 | 0 | |
| MetOp-A | 2.152 | -1.169e-06 | 0.396 | 0 | |
| Aqua | -0.341 | 0 | 0 | 0 | |
| Channel 8 | NOAA-15 | 0 | 0 | 0.667 | 0 |
| NOAA-16 | -5.043 | -1.768e-06 | 4.3 | 0 | |
| NOAA-17 | 2.078 | 0 | -1.099 | 0 | |
| NOAA-18 | 0.440 | 0 | 0.964 | 0 | |
| MetOp-A | 1.633 | 0 | 0 | 0 | |
| Aqua | -0.034 | 0 | 0 | 0 | |
| Channel 9 | NOAA-15 | 0 | 0 | 0.077 | 0 |
| NOAA-16 | -4.130 | -3.936e-07 | 2.3 | 0 | |
| NOAA-17 | 1.334 | 0 | -0.809 | 0 | |
| NOAA-18 | -0.108 | 0 | 0.820 | 0 | |
| MetOp-A | 0.111 | 0 | 1.246 | 0 | |
| Aqua | -1.403 | 0 | 0 | 0 | |
| Channel 10 | NOAA-15 | 0 | 0 | 0.346 | 0 |
| NOAA-16 | 0.227 | 0 | -0.200 | 0 | |
| NOAA-17 | 0.711 | 0 | -0.361 | 0 | |
| NOAA-18 | 0.876 | 0 | 1.116 | 0 | |
| MetOp-A | 0.975 | 0 | 1.148 | 0 | |
| Aqua | -0.189 | 0 | 0 | 0 | |
| Channel 11 | NOAA-15 | 0.532 | 0 | 0.251 | 0 |
| NOAA-16 | -0.788 | 2.910e-7 | 0.733 | 0 | |
| NOAA-17 | 0.595 | 0 | 0.406 | 0 | |
| NOAA-18 | 0 | 0 | 1.5 | 0 | |
| MetOp-A | 0.614 | 0 | 1.626 | 0 | |
| Aqua | 0 | 0 | 0 | 0 | |
| Channel 12 | NOAA-15 | 0 | 0 | 1.115 | 0 |
| NOAA-16 | -0.300 | -8.000e-7 | 1.600 | 0 | |
| NOAA-17 | 1.752 | 0 | 0 | 0 | |
| NOAA-18 | 3.390 | 0 | 0 | 0 | |
| MetOp-A | 3.662 | 0 | 0 | 0 | |
| Aqua | 1.754 | 0 | 0 | 0 | |
| Channel 13 | NOAA-15 | 0 | 0 | 1.500 | 0 |
| NOAA-16 | 0.702 | -8.045e-07 | 1.000 | 0 | |
| NOAA-17 | 1.471 | 0 | 0 | 0 | |
| NOAA-18 | 3.171 | 0 | 0 | 0 | |
| MetOp-A | 3.018 | 0 | 0 | 0 | |
| Aqua | 2.696 | 0 | 0 | 0 | |
| Channel 14 | NOAA-15 | ||||
| NOAA-16 | -1.364 | -0.154e-5 | 1.200 | 0 | |
| NOAA-17 | -0.514 | 0 | 0.712 | 0 | |
| NOAA-18 | 0 | 0 | 0.600 | 0 | |
| MetOp-A | -0.062 | 0 | -0.435 | 0 | |
| Aqua | 0 | 0 | 0 | 0 | |
Due to geometry of the NOAA polar-orbiting satellites, the SNO matchups are available only over the polar regions, where the brightness temperature range is slightly smaller than it is globally. Nevertheless, the calibration coefficients obtained from these matchups are applied globally for the entire life cycle of an MSU satellite. Using the obtained calibration coefficients, a global level-1c radiance dataset is generated from Eq. (1). Next, a limb correction is applied to these radiances to correct different incident angles of the off-nadir footprints to the nadir direction. This correction is necessary so that the off-nadir footprints can be used in the time series to increase observation samplings and reduce noise and sampling-related biases. The limb correction coefficients are obtained using a statistical method developed by Goldberg et al. (2001) based on global NOAA-10 observations during January 1987 (for MSU) and global NOAA-15 observations during July 1998 (for AMSU-A).
After the limb correction, a diurnal-drift correction was applied to the MSU channel 2 data over land to adjust the observations of any time to a local noon 12:00 clock. Currently, we use diurnal anomaly datasets developed by Remote Sensing System (RSS) for this correction. A scaling factor of 0.875 was used to multiply the RSS anomaly dataset to minimize intersatellite biases over land for MSU channel 2; A scaling factor of 0.917 was used to multiply the RSS anomaly dataset to minimize intersatellite biases over land for AMSU-A channel 5.
The corrected radiances are binned together to generate a pentad Tb dataset with grid resolution of 2.5° latitude by 2.5° longitude. A total of seven near-nadir footprints per scan line are used in the gridded time series. The SNO-calibrated level-1c scene radiances, limb-corrected radiances, and the merged gridded dataset can be downloaded directly through this website. For details on the calibration algorithm description, method to obtain calibration coefficients and merged gridded time series, please refer to:
Zou, C., M. Goldberg, Z. Cheng, N. Grody, J. Sullivan, C. Cao, and D. Tarpley (2006), Recalibration of Microwave Sounding Unit for climate studies using simultaneous nadir overpasses, J. Geophys. Res., 111, D19114, DOI: 10.1029/2005JD006798.
Zou, C.-Z., M. Gao, and M. Goldberg (2009), Error Structure and Atmospheric Temperature Trends in Observations from the Microwave Sounding Unit, J. Climate, 22, 1661-1681, DOI: 10.1175/2008JCLI2233.1
