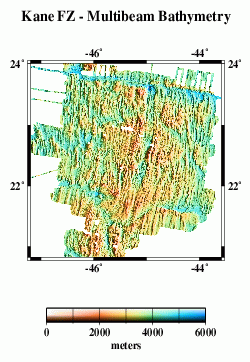
Multibeam Swath Bathymetry - Kane FZ
Geophysical Analysis
Data
Grid Information:
- West = -47.2
- East = -43.58
- South = 20.82
- North = 24
- Grid Nodes: nx = 1811, ny = 1591
- Depth: Max = 6119 m, Min = 1046 m
GMT command line arguments:
- -R-47.2/-43.58/20.82/24
- -I.002/.002
Grid Files:
- .CDF (masked), (GZ, 7.03 MB)
Data Source:
- This grid was compiled from 200 m grid areas 2, 3, 4, and 5 from the LDEO Ocean Floor Dataset (now the Global Multi-Resolution Topography Data Portal).
Profile Comparisons
Here we compare profiles from swath bathymetry (A) with estimated bathymetry (B), and satellite-derived gravity anomalies (C). Because there are limited constrainted points (black dots in E) in the estimated bathymetry along the profile (red line), and because of the resolution limit of the altimeter data used in the bathymetry prediction, the estimated anomalies do not resolve short-wavelength seafloor features evident in swath bathymetry (G).
| A | 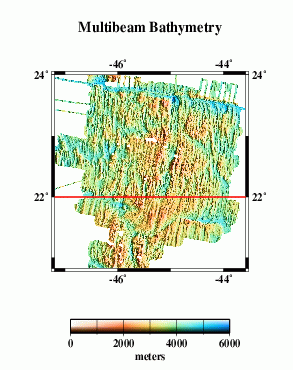 |
B | 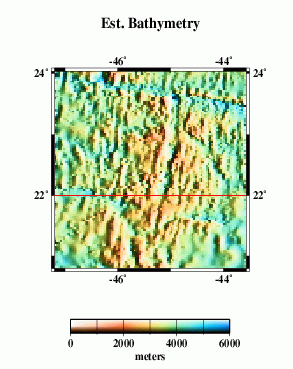 |
C | 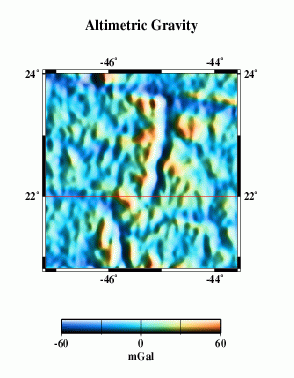 |
|---|
| D | 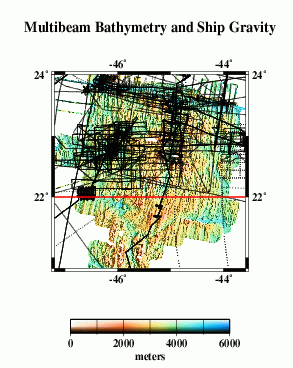 |
E | 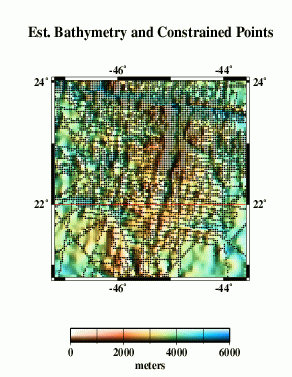 |
F | 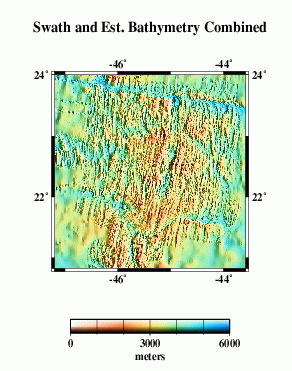 |
|---|
| G | 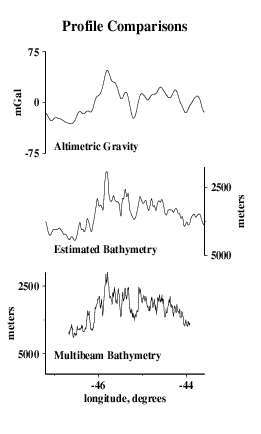 |
|---|
Grid Analysis
We compare the difference between altimetry-estimated bathymetry (2 min. grid) and actual swath bathymetry (.002 deg. grid) two ways, because the two are on grids of different spacing and thus may capture different length scales of bathymetric roughness.
For the lower-resolution analysis (H and I), multibeam data were averaged into corresponding 2-arc-minute blocks, and estimated bathymetry was subtracted. For the higher-resolution analysis (J and K), bilinear interpolation was used to obtain estimated bathymetry values at each point on the swath bathymetry grid, then the estimated bathymetry was subtracted.
In both cases, we find the mean difference is ~ 22 m (the swath bathymetry data are systematically deeper); the difference is about 0.6% of the depth. An error like this is expected because of the uncertainties in whether or not data sets used in calibration have been corrected for the variable speed of sound in seawater, errors translating uncorrected sound speeds between nominal fathoms and nominal meters, etc.
The standard deviations about the mean are 154 m for the 2 arcmin averages and 174 m for the multibeam points.
Since 174² - 154² ~= 81²,
We may assume that the root-mean-square (rms) average roughness captured by the multibeam and not capturable on a 2 arcmin grid is about m. The rms difference at longer scales, 174 m, is due to incomplete information in the estimated bathymetry grid.
| H | 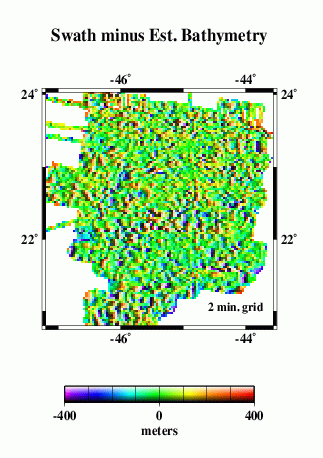 |
I | 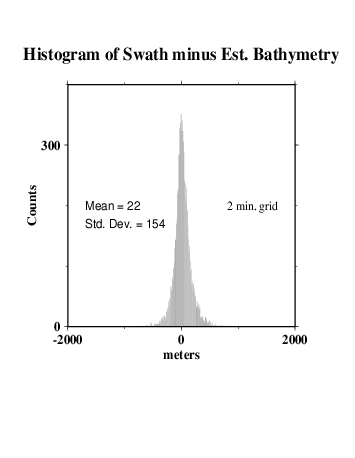 |
|---|
| J | 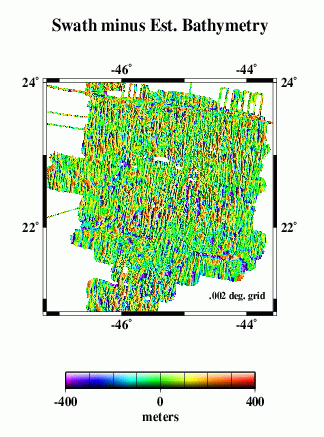 |
K | 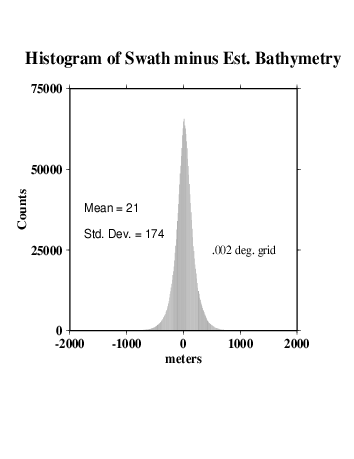 |
|---|
Eventually, we want to do a detailed cross-spectral analysis to determine how much of the actual multibeam bathymetry is captured in the altimeter gravity field. Here, we present a very simplified model. We take the combined bathymetry (F) and simply calculate a model gravity field, assuming that all the topography has the same density and is entirely uncompensated. This model (M) does not look much like the observed gravity (L), because our assumptions are too simple. The radially-averaged power spectra of the two (N) give some clue as to why.
At wavelengths longer than ~160 km or so, the simple model has too much power, because it does not include the effects of isostatic compensation of the topography. Between perhaps 20 and 120 km wavelengths, the two spectra are similar. then at shorter wavelengths the model again has more power than the altimetric gravity. Some of this is due to smoothing in the altimeter data necessary to remove noise. However, we don't know whether the simple model is realistic at these wavelengths. We need high- quality ship gravity data to compare, such data cover only about half of the study area.
| L | 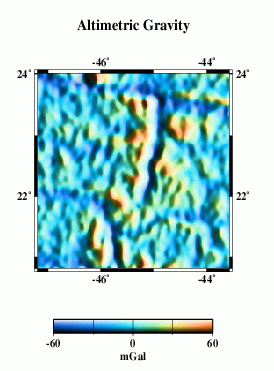 |
M | 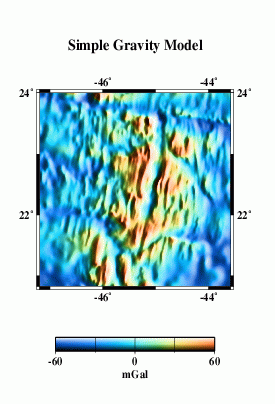 |
N | 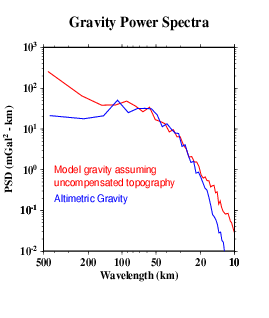 |
|---|