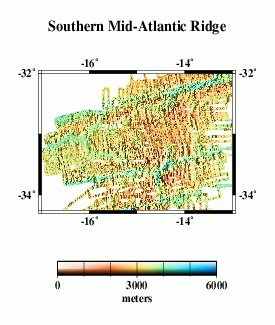
Multibeam Swath Bathymetry - Southern Mid-Atlantic Ridge
Geophysical Analysis
Data
Grid Information:
- West = -17
- East = -13
- South = -34.25
- North = -32
- Grid Nodes: nx = 2401, ny = 1351
- Depth: Max = 4960 m, Min = 1088 m
GMT command line arguments:
- -R-17/-13/-34.25/-32
- -I.00166667/.00166667
Grid Files:
- .CDF (masked), (GZ, 7.93 MB)
Data Source:
- These data were compiled by Gregory Neumann at the MIT Department of Earth, Atmospheric, and Planetary Sciences, and at the NASA Goddard Space Flight Center Laboratory for Terrestrial Physics, from cruises MRTN10, MRTN13, PLUME04, PLUME05 (T.Washington) and KN145L17 in 1984, 1985, 1990, and 1995.
- References:
- G. A. Neumann, P. J. Michael and B. B. Hanan, "Temporal variation of crustal emplacement, 33° S Mid-Atlantic Ridge," J. Conf. Abs., 1, 836-837, 1996.
- P. J. Michael, D. W. Forsyth, D. K. Blackman, P. J. Fox, B. B. Hanan, A. J. Harding, K. C. Macdonald, G. A. Neumann, J. A. Orcutt, M. Tolstoy and C. M. Weiland, "Mantle control of a dynamically evolving spreading center: Mid-Atlantic Ridge 33° S," Earth Planet. Sci. Lett.,, 121, 451-468, 1994.
- B. Y. Kuo and D. W. Forsyth, "Gravity anomalies of the ridge-transform system in the South Atlantic between 31 and 34.5° S: Upwelling centers and variations in crustal thickness," Mar. Geophys. Res., 10, 205-232, 1988.
Profile Comparisons
Here we compare profiles from swath bathymetry (A) with estimated bathymetry (B), and satellite-derived gravity anomalies (C). Because there are limited constrainted points (black dots in E) in the estimated bathymetry along the profile (red line), and because of the resolution limit of the altimeter data used in the bathymetry prediction, the estimated anomalies do not resolve short- wavelength seafloor features evident in swath bathymetry (F).
| A | 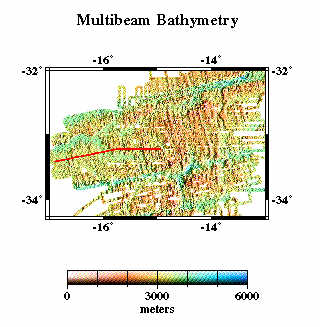 |
B | 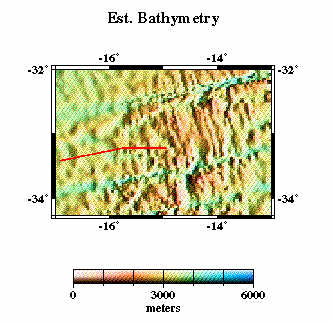 |
C | 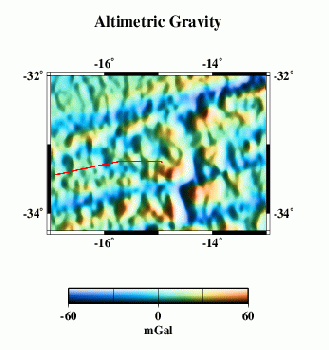 |
|---|
| D | 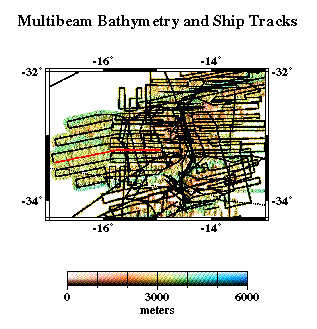 |
E | 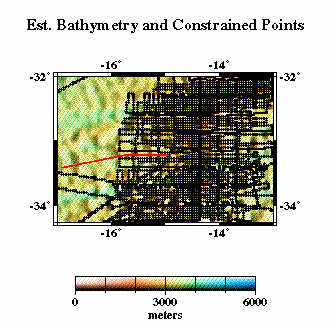 |
F |  |
|---|
| G | 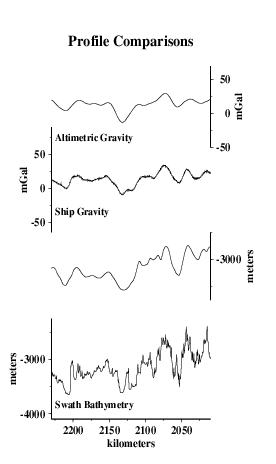 |
|---|
Grid Analysis
We compare the difference between altimetry-estimated bathymetry (2 min. grid) and actual swath bathymetry (.1 min. grid) two ways, because the two are on grids of different spacing and thus may capture different length scales of bathymetric roughness.
For the lower-resolution analysis (H and I), multibeam data were averaged into corresponding 2-arc-minute blocks, and estimated bathymetry was subtracted.
For the higher-resolution analysis (J and K), bilinear interpolation was used to obtain estimated bathymetry values at each point on the swath bathymetry grid, then the estimated bathymetry was subtracted.
In both cases, we find the mean difference is ~ 19 m (the swath bathymetry data are systematically shallower); the difference is about 0.6% of the depth. An error like this is expected because of the uncertainties in whether or not data sets used in calibration have been corrected for the variable speed of sound in seawater, errors translating uncorrected sound speeds between nominal fathoms and nominal meters, etc.
The standard deviations about the mean are 113 m for the 2 arcmin averages and 129 m for the multibeam points.
Since 129² - 113² ~= 62²,
We may assume that the root-mean-square (rms) average rounghness captured by the multibeam and not capturable on a 2 arcmin grid is about 62 m. The rms difference at longer scales, 129 m, is due to incomplete information in the estimated bathymetry grid.
| H | 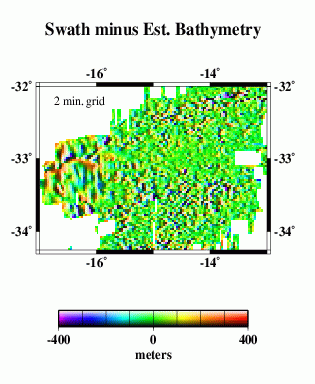 |
I | 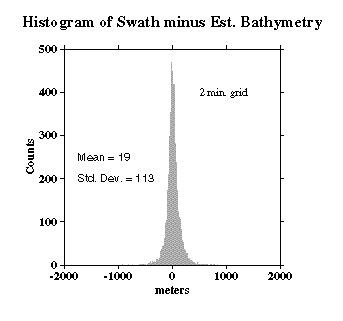 |
|---|
| J | 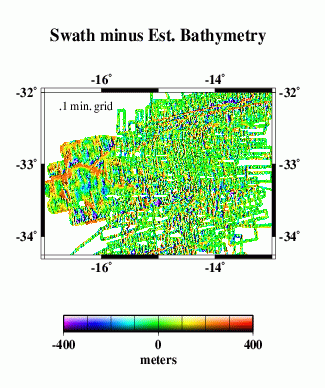 |
K | 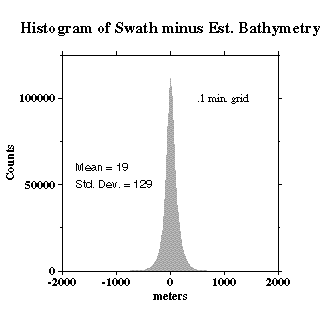 |
|---|
Eventually, we want to do a detailed cross-spectral analysis to determine how much of the actual multibeam bathymetry is captured in the altimeter gravity field. Here, we present a very simplified model. We talke the combined bathymetry (F) and simply calculate a model gravity field, assuming that all the topography has the same density and is entirely uncompensated. This model (M) does not look much like the observed gravity (L), because our assumptions are too simple. The radially-averaged power spectra of the two (N) give some clue as to why.
At wavelengths longer than ~160 km or so, the simple model has too much power, because it does not include the effects of isostatic compensation of the topography. Between perhaps 15 and 120 km wavelengths, the two spectra are similar. then at shorter wavelengths the model again has more power than the altimetric gravity. Some of this is due to smoothing in the altimeter data necessary to remove noise. However, we don't know whether the simple model is realistic at these wavelengths. We need high- quality ship gravity data to compare.
| L | 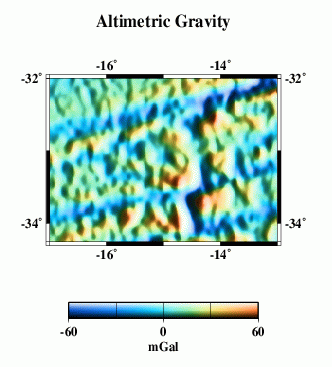 |
M | 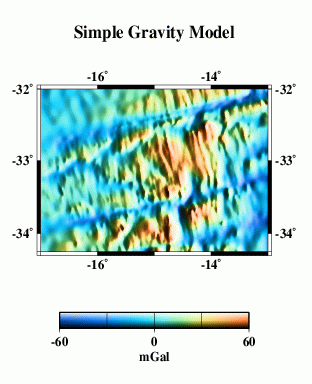 |
N | 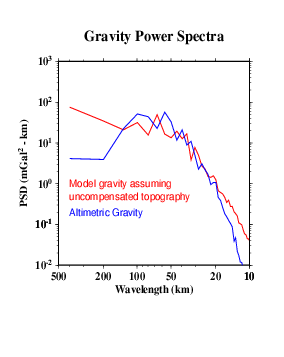 |
|---|