Microwave Integrated Retrieval System (MIRS) - Mathematical Background

The basis for the inversion problem is to find a vector X, in this case, a set of geophysical parameters, given a vector of measurements Y^m, in this case a vector of radiometric data (radiances or brightness temperatures). Different techniques are available in the literature. The validity of which mainly depends on the nature of problem. These techniques have different names but generally result in the same mathematical expressions. Among the names found in the literature are: maximum probability solution (MPS), variational retrieval (1D-VAR), Bayesian algorithm, Optimal Estimation Theory, etc. For the purpose of describing the mathematical basis of MIRS, we will follow the probabilistic approach as it will highlight two important points in the assumptions made for this type of retrievals; Namely, the local- linearity of the forward problem, as well as the Gaussian nature of both the geophysical state vector and the simulated radiometric vector around the measured vector.

General Inverse Solution

In what follows, the problem is posed in general terms. Each time a hypothesis is made, it is highlighted in bold with a superscript attached to it. The resulting mathematical formulation of the inverse problem will therefore be always valid provided those assumptions satisfied. Intuitively, the retrieval problem amounts to finding the vector X which maximizes the probability of being able to simulate Y^m using X as an input and Y as the forward operator. This translates mathematically into maximizing:

P(X|Y^m)

(1)

The Bayes theorem states that the joint probability P(X,Y) could be written as:

P(X,Y)=P(Y|X)xP(X)=P(X|Y)xP(Y)

(2)

Therefore, the retrieval problem amount to maximizing:

(3)

Because we are in a situation where the measurements vector Y^m exists, it is therefore evident that

P(Y^m)=1

(4)

It is generally assumed that X follows a Gaussian¹ distribution. If we assume for a moment, for the sake of simplicity, that X is a monovariate vector, with a mean value X₀ and a standard deviation σ, then the Probability Density Function (PDF) of its Gaussian distribution could be written as:

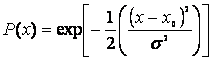
(5)

or more generally, for a multivariate vector:

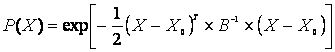
(6)

Where X₀ and B are the mean vector and covariance matrix of the vector X respectively.

Ideally, the probability P(X|Y^m) is a Dirac function with a value of zero except for X. Modeling errors and instrumental noises all influence this probability. For simplicity, it is assumed that the PDF of P(X|Y^m) is also a Gaussian² function with Y(X) as the mean value (i.e., the errors of modeling and instrumental noise are non-biased³), that could be written as:

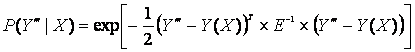(7)

E is the measurement and/or modeling error covariance matrix. Y is a forward operator⁴ capable of simulating a measurements-like vector.

So, maximizing P(X|Y^m) is equivalent to maximizing P(X|Y^m)xP(X) or:

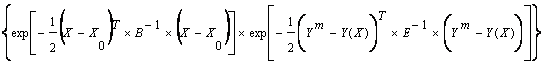(8)

It is obvious that it is easier to maximize the logarithm ln(P(X|Y^m)) instead, or minimize -ln(P(X|Y^m)) which would amount to minimizing:

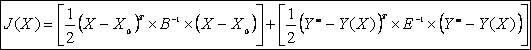(9)

J(X) is generally called the cost function. The left term represents the penalty in departing from the background value (a-priori information) and the right term represents the penalty in departing from the measurements. The solution that minimizes this two-terms cost function is sometimes referred to as a constrained solution. The minimization of this cost function is also the basis for the variational analysis retrieval. The solution that minimizes this cost function is easily found by solving for:

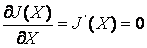(10)

For the sake of illustration, let us consider the monovariate case again. The cost function is written in this case, as:

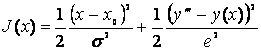(11)

Where e is the standard deviation of the modeling/measurement errors distribution. So, minimizing this cost function amounts to:

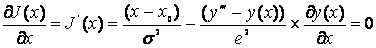(12)

At this stage, we make another assumption about the forward operator Y; We assume it is locally linear5 around X. For the simple case, this translates into:

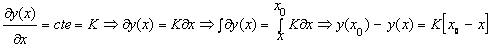(13)

Therefore:

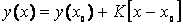(14)

If we apply the above to the general case, we obtain:

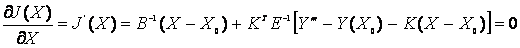(15)

Or,

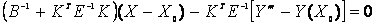(16)

Which results into the following:

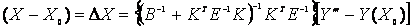(17)

If we keep in mind that:

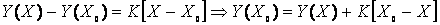(18)

And if we ingest the above equations into an iterative loop, each time assuming that the forward operator is linear, we could end up with the following iterative solution to the cost function minimization process:

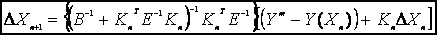(19)

Where n is the iteration index. The previous solution could be rewritten in another form after matrix manipulations:

(20)

Although equations 19 and 20 are equivalent mathematically, we can notice that equation 20 is more efficient because it requires the inversion of only one matrix. Generally, the first formulation is used in the infrared interferometry because the number of parameters is much smaller than the number of channels while the second formulation is more often used when the number of channels is smaller than the number of parameter to retrieve which is the case of the microwave in general. Equation 20 is currently implemented in MIRS. At each iteration n, we compute the new optimal departure from the background given the current geophysical and radiometric departures, the derivatives as well as the covariance matrices (error/modeling covariance and the geophysical covariance). This is an iterative-based numerical solution that accommodates slightly non-linear problems or parameters with slightly non-Gaussian distributions. This approach to the solution is generally labeled under the general term of physical retrieval. The Microwave Integrated Retrieval System (MIRS) performs the retrieval in one loop as detailed in next section. The whole geophysical vector is retrieved as one entity, ensuring a consistent solution that fits the radiances. The constraints are in the form of the measurements as well as the assumed a-priori information.